While there is (^) Caret Arithmetic Operator to compute the value having power like (5²), it can make calculations more complex for long equations. Imagine rewriting the caret sign like this 5^5^5^5^5^5^5^5^5^5 for (510). It would make your equations look cluttered and messy.
In such case, you can use Excel’s POWER Function to simplify your work. It is one of the Math & Trigonometric functions used for solving exponential equations. We have compiled a detailed guide about the POWER Function in this article.
Arguments for POWER Function
The POWER Function gives the output of a number raised to an exponent number. There are two arguments for the POWER function. Here, the Number is a base number and Power is an exponent number which raises the base number to.
Syntax: POWER(number, power)
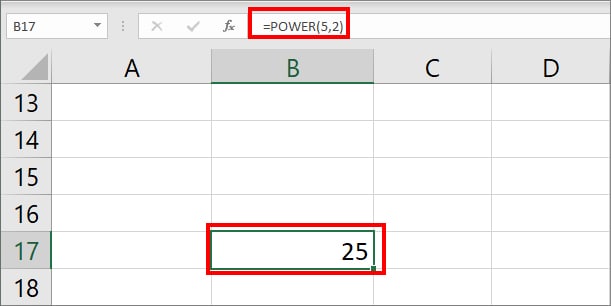
For Example: 5²
To raise the base number 5 by power 2, the formula would be =POWER(5,2). It returns 25 as an output.
Let’s take a look at more examples of the Power function in different scenarios below.
| Formula | Result | Description |
| =POWER(3,3) | 27 | In this example, the Power function will raise the number 3 by power 3 and return 27 as an output. 3³ = 3 * 3 * 3 = 27 |
| =POWER(25,½) | 5 | ½ is one of the fractional exponents. Here, when we raise the number 25 by ½ you get 5 as a result. 25½ = 25 ^ 0.5 = 5 |
Where to Best Use the POWER Function
Solve Math Equations
Excel is the best calculator for solving any mathematical equations. You could use the POWER Function to perform exponential problems.
Suppose, y=x^n is the given equation and you need to find out the value of y from the following information.
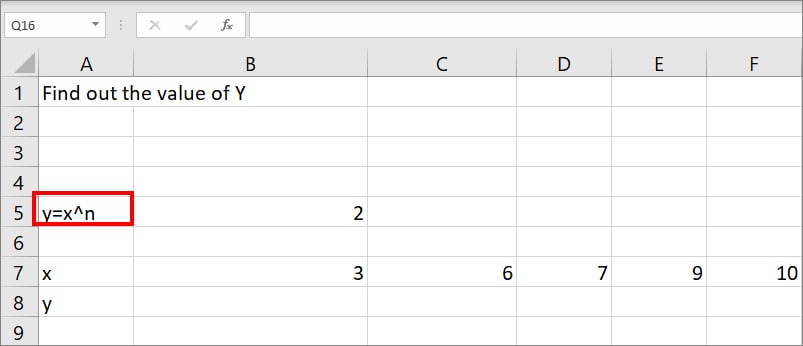
For this, enter =POWER(B7,$B$5) formula in the B8 cell. Here, B7 is the value of x and $B$5 is the value of n.
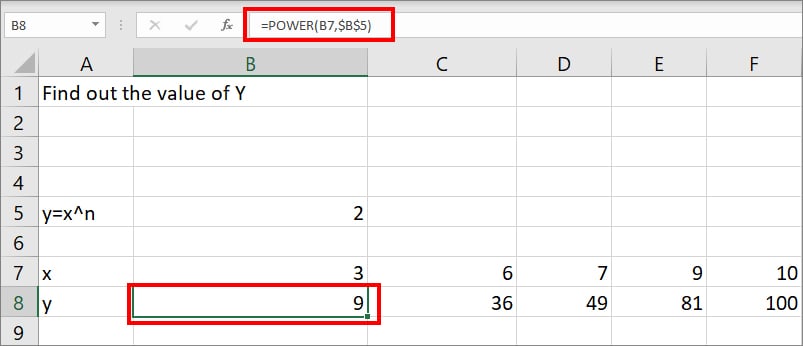
You might have noticed a dollar sign in the B5 cell. This implies that the cell reference is an Absolute cell reference which allows you to use the flash fill for other ranges.
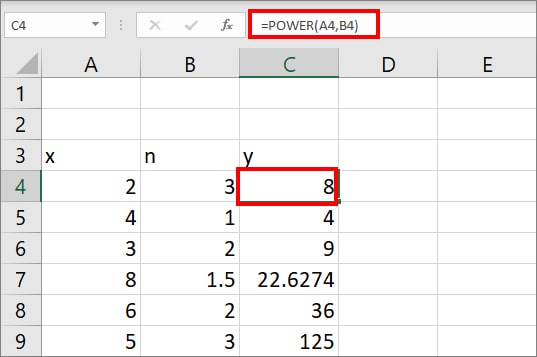
However, if you have to calculate the equation from the following data that has relative cell references, enter =POWER(A4,B4) formula in cell C4.
Quadratic Equations
Apart from calculating simple exponential equations, you can also use the POWER Function to solve Quadratic Equations.
The formula of the Quadratic Equation is x= (-b+(b2-4ac)½)/2a, x= (-b-(b2-4ac)½)/2a.
Suppose, you need to find out the two square root values from the given equation: 2x2+5x+3=0 . When you place the coefficient value in the Quadratic formula, it would be as shown in the image.

To determine the value in Excel, we will combine it with the POWER function.
For 1st root enter, =((-5+POWER(POWER(5,2)-(4*2*3),1/2)))/(2*2)formula. You will get -1 as output.
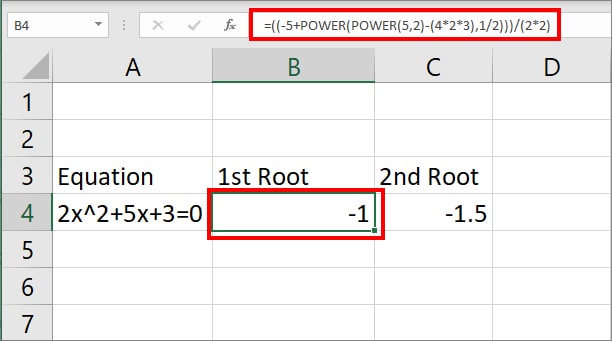
To find out 2nd root, enter =((-5-POWER(POWER(5,2)-(4*2*3),1/2)))/(2*2). It will return -1.5 output.
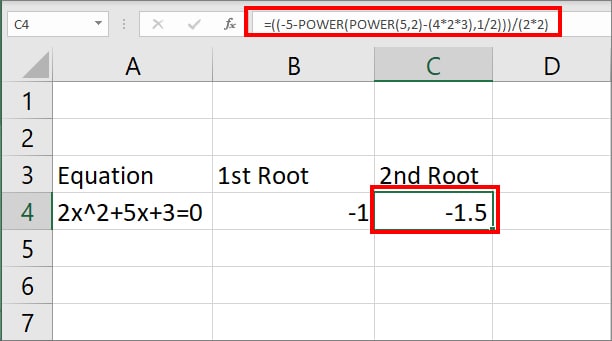
Let’s check how the formula works.
- Here, the POWER function first returns the value of 52 i.e. POWER(5,2).
- Then, POWER Function takes (25-(4*2*3) as number and ½ as power i.e. POWER( (25-(4*2*3),1/2))
Calculate Compound Interest
Excel is one of my go-to software for managing personal finances. I use it for calculating almost everything related to finance like summing up monthly expenses, finding out compound interests, etc. The best part is I can enter the formula just once and then copy it down for obtaining the rest of the results.
Another effective use of the POWER Function is to calculate the Compound Interest. Since the formula is A = P(1+r/n)nt, this function simplifies the process of computing the exponents by taking values as numbers and power arguments.
Let’s assume you need to calculate the compound interest of an annual investment of $1000 at 5% after 7 years. Here, Principal (P) =1000, Rate(r) =5%, Time = 7 years, and Compounded yearly (n)=1 as shown in the given picture.
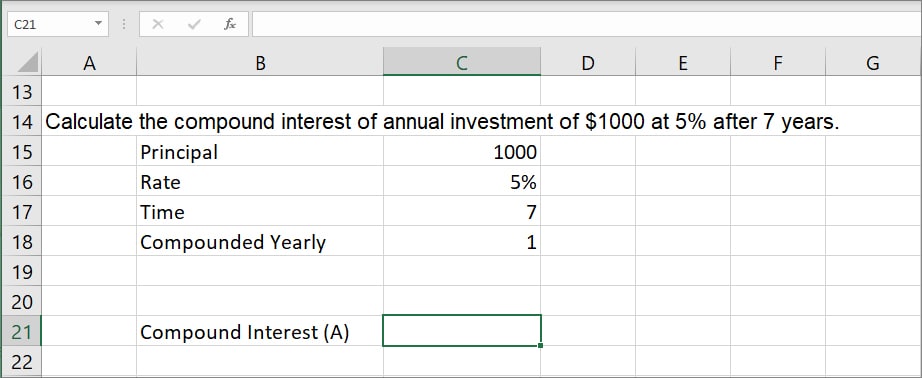
For this, we will create a combined formula using the POWER function and Compound Interest Formula.
According to the data, enter =C15*(POWER((1+(C16/C18)),(C17*C18))) formula. It will return 1407.1 as result.
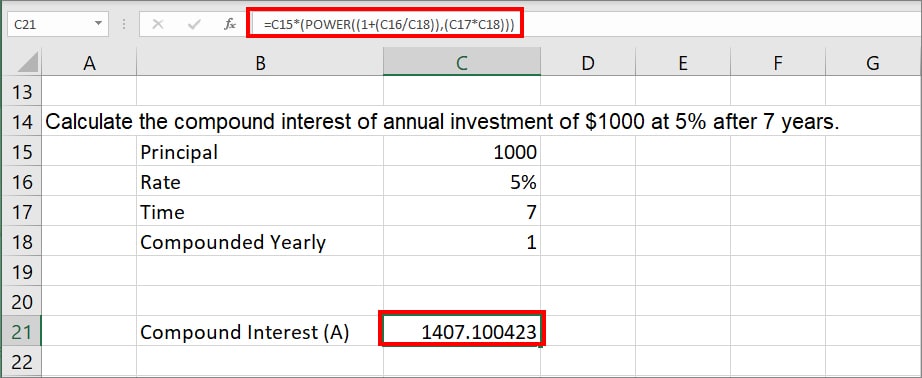
In the above formula, the POWER function takes up two arguments: (1+(C16/C18)) is Number, and (C17*C18) is Power. Then, the returned value is multiplied by C15 i.e. Principal amount.
Solve Physics
Applications of Exponents are not limited to Maths and Algebra. You can find them in Science equations too. So, another use of the POWER function is to solve Physics equations. Yes, you heard that right! Let’s check it out.
Let’s assume you need to determine the Gravitational Force between the earth’s 5.45 * 1024 kg and a 60 kg boy who is standing at sea level, a distance of 2.3 * 105m from the earth’s center. Gravitational Constant Value is 6.35 * 105Nm2kg-2.
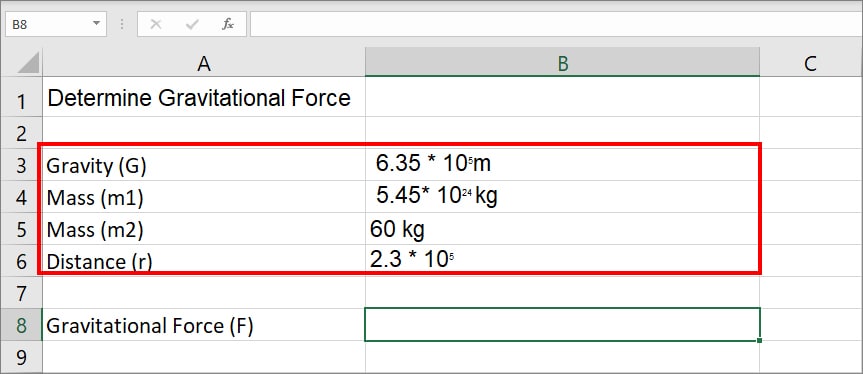
The formula for Gravitational Force (F)= Gm1m2/r2. We will combine this formula using the POWER function to solve the equation.
Formula:
=((6.35*POWER(10,5))*5.45*POWER(10,24)*60)/POWER(2.3*POWER(10,5),2)
Let’s see how this formula works first.
| Gravitational Force Formula Components | Formula | Description |
| G | ((6.35*POWER(10,5)) | This formula returns the value of Gravitaional force (G) 6.35 * 105Nm2kg-2. The POWER Function takes 10 as number and 5 as power. Then, multiplies 6.35. |
| m1m2 | 5.45*POWER(10,24)*60) | Here, the formula returns the value of m1m2. For, m1 (5.45 * 1024 )the POWER function takes 10 as the number and 24 as Power. Then, multiplies 5.45. Again, the returned value is multiplied by m2 (60). |
| r2 | POWER(2.3*POWER(10,5),2) | This formula calculates the value of r (2.3 * 105m) using the POWER function i.e. 2.3*POWER(10,5). Then, returns r2 as a final result. Here, the POWER Function takes the returned value as a number and 2 as power i.e. POWER(number, 2). |
You will get 3925236294896030000000 as a final result.
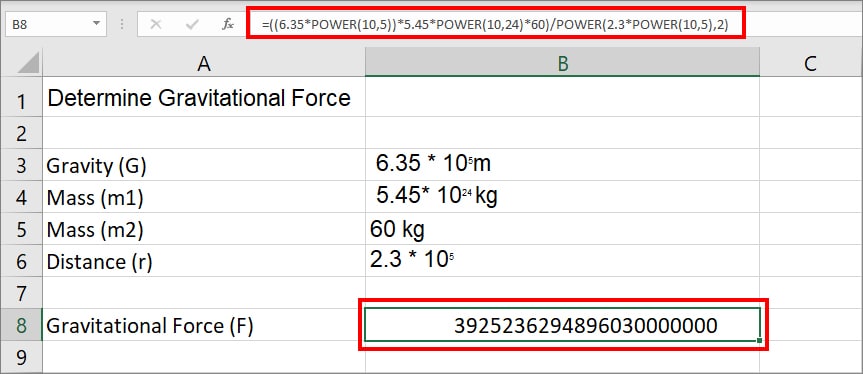
Note: We converted the final output into Fraction format from the Number section of the Home Tab.